민트초코 먹고싶다
'음악' 카테고리의 다른 글
| 2019 M3 Autumn 앨범 구매 (0) | 2019.10.29 |
|---|---|
| ねぇ?メイドさんはみんな忠実だと思う? (0) | 2019.07.22 |
| Porter Robinson & Madeon - Shelter (0) | 2018.07.13 |
| 너의 은빛 정원 (君の銀の庭) (0) | 2018.07.10 |
민트초코 먹고싶다
| 2019 M3 Autumn 앨범 구매 (0) | 2019.10.29 |
|---|---|
| ねぇ?メイドさんはみんな忠実だと思う? (0) | 2019.07.22 |
| Porter Robinson & Madeon - Shelter (0) | 2018.07.13 |
| 너의 은빛 정원 (君の銀の庭) (0) | 2018.07.10 |
이제 BX를 trello 를 사용해서 관리합니다.
압축은 UTF-8로 되어 있으니, 이를 지원하는 어떤 프로그램으로 풀어도 상관 없습니다. (Bandizip 등)
패키지를 모두
https://bms.kyouko.moe/ 로 옮겼습니다. 아래 링크는 2020년 5월 이후에 삭제하겠습니다.
=== 이전 게시글 ===
Satellite(2020-03-01): https://bms.kyouko.moe/package/Satellite.html
통상 (17.7GB): https://bms.kyouko.moe/package/Normal.zip
델타 (9.4GB): https://bms.kyouko.moe/package/Delta.zip
Overjoy (구버전 신버전 포함, 6.1GB): https://bms.kyouko.moe/package/Overjoy.zip
발광 (22.4GB): https://bms.kyouko.moe/package/Insane.zip
Stella (2020-03-01): https://bms.kyouko.moe/package/Stella.html
통합 패키지: https://blog.kyouko.moe/48
UPD: 서버가 2020년 1월 4일 오전 10:00 부터 오후 3:00 까지 서버 이전 때문에 접속이 안 될 것입니다.
| BMS Archive 개발 근황 (0) | 2020.01.19 |
|---|---|
| 서버 근황 (0) | 2019.12.07 |
| [BX 개발기] 1. BMS 제목/아티스트 추출 (0) | 2019.08.14 |
| 개인 홈페이지에 SSL 인증서를 달았습니다! (0) | 2018.07.27 |
| 비트연산과 집합 (0) | 2017.11.25 |
https://github.com/ho94949/bms-archive
BMS archive service 의 약자는 BX로 정해졌습니다! archive 를 줄여서 arXiv로 부르는 https://arxiv.org 에서 따왔습니다.
일단 오늘 구현한 것은 BMS파일의 제목 및 작곡가 추출입니다. 유저단에서 돌릴 것은 아니므로 에러가 아예 안 날 필요는 없으나, 최대한 예외처리를 하는 방향으로 진행했습니다.
BMS 파일은 제목과 아티스트를 설정하게 되어있고, 대부분의 BMS에서는 제목에 난이도 이름까지 넣는 경우가 대부분입니다.
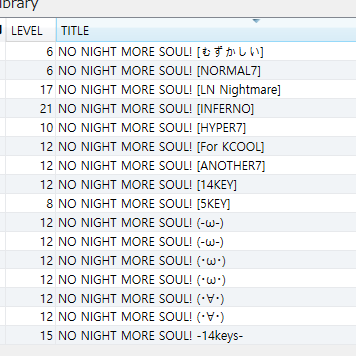
여기서 우리는 노래 제목이 NO NIGHT MORE SOUL! 이라는 것을 알 수 있지만, 이것을 추출하는데 일련의 로직이 있어야 합니다.
제가 구현한 방법은 일단 IMPLICIT SUBTITLE을 모두 제거하는것 입니다. IMPLICIT SUBTITLE은 제목 안에 있는 [], (), -- 등으로 둘러싸인 다른 제목들을, 암시적으로 구분하는 것을 말하며 보통 난이도 등을 표시할 때 많이 쓰이기 때문에, 이것을 제외하면 노래 제목이 나오는 경우가 많습니다. 지금은 #SUBTITLE이란 명령이 있기는 하지만, 대부분 그냥 #TITLE 에 달아놓는것 같습니다.
가끔 곡 뒤에 이상한 SUBTITLE을 넣는 경우가 있고, 노래 제목 뒤에 이상한것을 붙이는 경우도 많기 때문에 제가 선택한 방법은 다음과 같습니다.
1. 모든 IMPLICIT SUBTITLE을 제거합니다.
2. 가장 짧은 제목을 찾습니다.
3. 이 제목이 모든 제목의 접두사인지 확인합니다.
이 방법을 통해서 대부분의 노래는 구분할 수 있습니다. 물론 너무나도 많은 예외들이 있습니다.

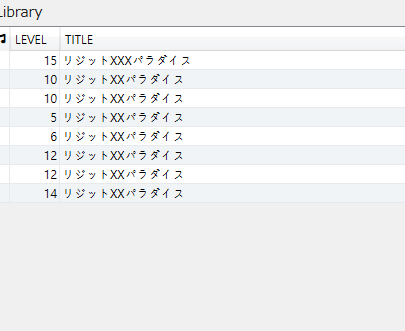


그래서 이런 노래들에는 임시로 N/A를 붙여놓고 수동으로 이름을 붙여주는 수 밖에 없을 것 같습니다.
뭔가 규칙들을 좀 더 정리해 나가면 좋을것 같다는 생각은 들긴 듭니다.
| 서버 근황 (0) | 2019.12.07 |
|---|---|
| [BX 개발기] 2. BMS 차분 모으기 / 패키지 (0) | 2019.08.30 |
| 개인 홈페이지에 SSL 인증서를 달았습니다! (0) | 2018.07.27 |
| 비트연산과 집합 (0) | 2017.11.25 |
| [ACM-ICPC] KAIST Deobureo Minkyu Party 팀노트 (0) | 2017.11.22 |