SCPC 2021 2차 대회가 8월 7일 오전 9시부터 12시간동안 진행되었다.
SCPC 대회와 관련된 정보는 https://research.samsung.com/scpc 에서 찾을 수 있다.
이 게시글에서는 해당 대회 문제의 풀이를 다룬다.
1. 원 안의 점
문제를 요약하면, 원점 $(0, 0)$을 중심으로 하는 반지름 $R$인 원 내부에 들어있는 좌표가 모두 정수인 점의 개수를 세는 문제이다. 단, 원의 경계에 놓인 점은 생각하지 않는다. ($R \le 200\,000$)
풀이는 간단하다. $x$좌표가 $a$인 위치에 대해서 $y$좌표로 가능한 값은 $-\sqrt{x^2-a^2}$ 초과 $\sqrt{x^2-a^2}$ 미만인 값이고($-R < a < R$), 정수점의 개수는 $\sqrt{x^2-a^2}$ 미만인 양의 정수의 개수에다가 1을 곱한 값이다. 구현할 때는 $\sum_{a=-R+1}^{R-1} (\lfloor \sqrt{x^2-a^2-1} \rfloor$)과 같은 식으로 구현할 수 있다. ($x^2-a^2$은 정수이기 때문에, $x^2-a^2$ 미만인 정수는 $x^2-a^2-1$ 이하인 정수와 같다.)
시간복잡도는 $\mathcal{O}(R)$이다.
2. 직8각형

문제를 요약하면, 한 변의 길이가 $K$인 각 변이 축에 평행한 정사각형 5개가 그림처럼 +모양으로 배치되어 있을 때, 외각에 놓인 8개의 점을 길이가 $K$인 직8각형이라고 부른다. 평면 상의 점 8개와 $K$가 주어질 때, 길이가 $K$인 직8각형이 되도록 점을 옮기려고 한다. 여기서, 점의 순서는 중요하지 않다. 이 때, 필요한 점의 이동거리 합의 최소값을 구하는 문제이다. 여기서, 이동거리는 택시거리이다($(a, b)$와 $(c, d)$ 사이의 거리는 $|a-b| + |c-d|$이다.)
어떤 점이 직8각형의 어떤 점에 대응되어야 하는지 알 경우에 필요한 이동거리 합의 최솟값을 구하는 방법을 생각해보자.
첫째로, 택시거리는 $x$좌표와 $y$좌표의 차이의 합이기 때문에, $x$좌표와 $y$좌표를 따로 생각할 수 있다. 그렇기 때문에, $x$좌표와 $y$좌표에 대해 문제를 따로 따로 풀어줄 수 있다.
둘째로, 이동거리가 최소가 되는 $p_0$의 $x$좌표를 편의상 $a$라고 하면, $p_0, p_1$으로 옮기는 점은 $x$좌표가 $a$, $p_2, p_7$로 옮기는 점은 $x$좌표가 $a+K$, $p_3, p_6$으로 옮기는 점은 $x$좌표가 $a+2K$, $p_4, p_5$로 옮기는 점은 $x$좌표가 $a+3K$가 되도록 옮겨야 한다. $p_i$로 옮겨야 하는 점의 $x$좌표를 $x_i$라고 하면, $|x_0 - a| + |x_1 - a| + |x_2 - (a+K)| + |x_3 - (a+2K)| + |x_4 - (a+3K)| + |x_5 - (a+3K)| + |x_6 - (a+2K)| + |x_7 - (a+K)|$ 를 최소화 하는 문제가 된다. 기본적으로 어떤 배열 $v$에 대해, 합 $|v_i-a|$를 최소화하는 문제는 매우 잘 알려진 문제로, $a$를 $v_i$의 중앙값으로 잡으면 된다. 이 경우도 유사하게, $a$를 $x_0, x_1, x_2-K, x_3-2K, x_4-3K, x_5-3K, x_6-2K, x_7-K$의 중앙값으로 설정하면 될 것이다. $y$좌표에 대해서도 문제를 비슷하게 풀어줄 수 있다.
이런 식으로, 어떤 점이 직8각형의 어떤 점에 대응되어야 하는지 알 경우 필요한 이동거리 합의 최솟값은 $\mathcal{O}(8)$에서 $\mathcal{O}(8^2)$ 정도의 시간에 중앙값을 구해서 합을 구하는 방식으로 문제를 해결할 수 있다. 이제 모든 조합을 다 시도해보면 $\mathcal{O}(8! \times 8)$ 에서 $\mathcal{O}(8! \times 8^2)$ 정도 시간에 문제를 해결할 수 있다.
3. 산탄총

문제를 요약하면, $N \times N$ 격자의 각 칸에 (음수일 수 있는) 수가 하나 써 있고, 산탄총의 퍼지는 정도 $K$가 주어진다. 산탄총을 어떤 칸을 중심으로 사격하면 중심과 택시거리가 $K$ 미만인 칸에 대해서, 해당 칸과 중심의 택시거리가 $x$이면 해당 칸에 있는 수에 $K-x$를 곱한 수 만큼의 점수를 얻는다. 여기서, 중심은 격자 밖일수도 있다. 산탄총을 한번 사격해서 얻을 수 있는 점수의 최댓값을 구하는 문제이다. 오른쪽 그림은 $K=3$일때 산탄총을 사격해서 얻을 수 있는 점수의 모양이다. ($1 \le K \le N \le 600$)
모든 칸을 중심으로 해서 산탄총을 쐈을 때, 각각의 점수를 구해서 그 중 최댓값을 구하면 되는 문제이다. 격자의 밖을 중심으로 하는 경우도 물론 고려해야한다. 격자에서 $K$ 이상 떨어진 곳을 중심으로 산탄총을 사격하는 경우에는 점수가 항상 0이므로 고려하지 않아도 되고, 각 좌표가 $-K$ 부터 $N+K$인 곳을 고려해서 사격하면 된다.
이제, 각 칸의 점수를 효율적으로 구하기 위해서, 중심을 오른쪽으로 한 칸 옮길 때 점수 차이를 살펴보자. 두 칸의 경계를 기준으로 왼쪽에 있는 칸의 거리는 1씩 늘어나고, 오른쪽에 있는 칸의 거리는 1씩 줄어든다. 열 번호가 왼쪽 칸 이하이면서, 거리가 $K$미만인 칸(아래 그림에서 주황색 영역)의 수의 합만큼 값이 줄어들고, 열 번호가 오른쪽 칸 이상이면서, 거리가 $K$미만인 칸(아래 그림에서 파란색 영역)의 수의 합만큼 값이 늘어난다.
이제, 파란색 영역과 주황색 영역의 합을 효율적으로 구해보자. 파란색 영역의 중심칸을 아래로 한 칸 옮기면 거리가 $K-1$인 점들이 바뀌게 된다. 여기서 위쪽 칸과 거리가 $K-1$이면서, 열 번호가 위쪽 칸 이상이고, 행 번호가 위쪽칸 이하인 점들(아래 그림에서 빨간색 영역)의 수의 합 만큼 값이 줄어들고, 아래쪽 칸과 거리가 $K-1$이면서, 열 번호가 위쪽 칸 이상이고, 행 번호가 오른쪽 칸 이상인 점들(아래 그림에서 초록색 영역)의 수의 합 만큼 값이 늘어난다. 주황색 영역도 대칭적으로 구할 수 있다.
이제, 우리는 빨간색과 초록색으로 표현된 영역인 대각선 모양의 $K$개의 칸의 합을 효율적으로 구해야하는데, 이는 중심칸이 오른쪽 아래로 내려갔을 때, 왼쪽 끝과 오른쪽 끝의 수가 더해지고 빠지는 것으로 문제를 해결할 수 있다. (그림의 노란색과 보라색 칸) 초록색 영역도 대칭적으로 구할 수 있다.
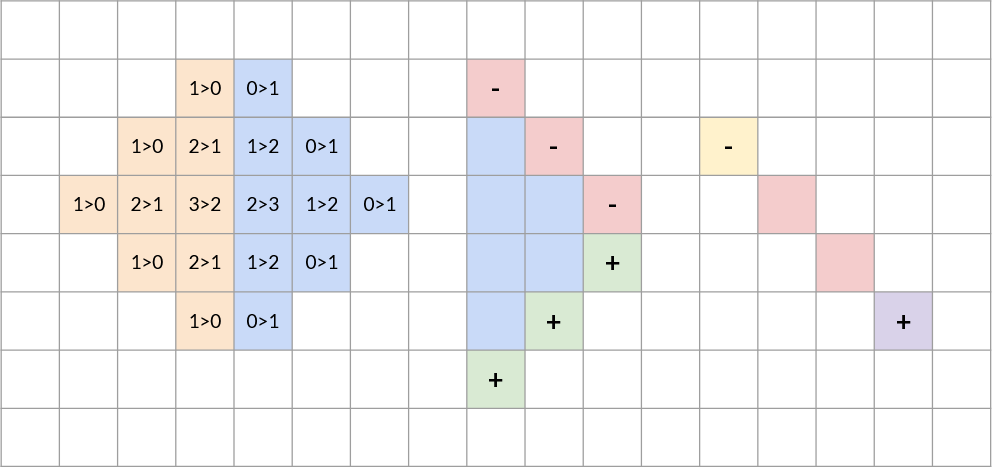
이 영역들의 합을, 좌표를 섬세하게 계산해주면 문제를 해결할 수 있다. 각 영역은 중심이 한 점에서 다른 점으로 옮겨질 때 상수번의 연산만을 하기 때문에, 시간 복잡도는 $\mathcal{O}(N^2)$이다.
4. 패턴 매칭
문제를 요약하면, 두 문자열 $A$와 $B$가 매칭된다는 것은, $A$와 $B$의 길이가 같고, $A_i = A_j$와 $B_i=B_j$가 동치라는 것을 의미한다. 텍스트 하나와 $K$개의 패턴을 주어질 때, 각 패턴이 텍스트에 등장하는 횟수를 계산하여라. (텍스트의 길이 $2\,000\,000$ 이하, 패턴의 길이 $500$이하, 패턴 길이 합 $30\,000$이하)
Aho-corasik의 패턴 매칭 알고리즘을 사용하자. 우리가 문자열의 각 문자 대신 매칭에 사용할 대상은 이전에 같은 문자가 언제 등장했는지 여부이다. 다음과 같은 관찰을 활용하자.
관찰. 어떤 문자열 $S$의 $f(S)$를 다음과 같이 정의하자.
- $f(S)$는 길이가 $S$와 같은 배열이다. $f(S)$의 $i$ 번째 값은 $S_i = S_{i-L}$을 만족하는 최소인 양수 $L$이다. (조건을 만족하는 $L$이 없을 경우 $f(S)$의 $i$ 번째 값은 0이다.)
문제에서 정의한 문자열 $A$와 $B$가 매칭되는 것은 $f(A)$와 $f(B)$가 동일한 것과 동치이다.
증명. (⇒) $f$를 정의할 때 사용한 연산은, 문자열의 두 값이 같다는 연산 뿐이기 때문에, 문제에서 주어진 $A$와 $B$에 대한 $f(A)$와 $f(B)$의 값은 동일하다.
(⇐) $A_i$와 같은 문자가 등장하는 $i$ 번째 이전의 위치를 찾아보자. $f(A)_i$가 0이면, 같은 문자가 등장하지 않는다. $f$의 정의에 따라, $A$의 $i-f(A)_i$ 번째 위치에서 $A_i$와 같은 문자가 등장하고, $i-f(A)_i$ 번째 위치에서 $i$번째 위치 사이에서는 문자가 등장하지 않는다. 이제 $i-f(A)_i$ 번째 위치 이전에서는 $A_i$와 같은 문자가 언제 등장하는지를 살펴보자. $A_{i-f(A)_i} = A_i$이기 때문에, $f(A)$ 배열의 $i-f(A)_i$ 값을 확인하는 것으로 재귀적으로 확인해 줄 수 있다.
$f(A)$와 $f(B)$의 값이 같다는 것은, $A_i$와 같은 문자가 등장하는 $i$ 번째 이전의 위치와, $B_i$와 같은 문자가 등장하는 $i$ 번째 이전의 위치의 집합이 같다는 뜻이다. 그렇기 때문에, $A_i = A_j$와 $B_i=B_j$는 동치이다.
이를 직접 사용하려고 하면, 위의 정의가 "길이가 다른 두 문자열"에 대해서는 동작하지 않는다는 것을 알 수 있다. 예를 들면 $S=abaca$와 $T=xyx$가 있다고 하자. $f(S)$는 $[0, 0, 2, 0, 2]$이고 $f(T)$는 $[0, 0, 2]$이다. 위에 정의한 문자열 매칭을 그대로 사용하면, $S$는 $T$의 첫 번째 위치에서만 매칭되는 것으로 생각되지만, 실제로는 세번째 위치에서도 매칭된다. 이는 부분문자열 $aca$와 $xyz$에서 첫번째 $a$에 해당하는 $f$값 $2$가 매칭되는 패턴 $xyz$의 $x$의 인덱스인 $0$보다 커서, $2$칸 전의 문자가 사실 같음에도 매칭할 때는 고려대상이 되지 않기 때문에 발생하는 문제이다. 특정 위치의 함수값이 인덱스보다 큰 경우는 고려 대상에서 제외해서 배열의 값을 $0$으로 바꿔줘야 하고, 이는 Aho-corasik의 failure function을 계산할 때 처리해 줄 수 있다.
이래서, (일반적인) 스트링 $f(T)$에서 패턴 $f(P)$가 언제 등장하는지 개수를 세는 문제로 바뀌었다. 기본적인 Aho-corasik 문제임으로 따로 설명하지는 않는다. 위의 failure function을 계산할 때, 자기보다 길이가 긴 인덱스 값이 등장하는 시점에 유의하자.
시간복잡도는 문자열 길이와 패턴 길이 합의 선형에 비례하는 시간복잡도가 든다.
5. Hanoi Tower
문제를 요약하면, 일반적인 하노이 타워 문제와 같이, 1번 기둥에 있는 원판을 3번 원판으로, 큰 디스크가 작은 디스크 위에 올라가지 않도록 모두 옮기는 문제이다. 단, 기존 하노이 타워는 한 기둥에서 다른 기둥으로 옮길 때, 한 기둥의 첫 번째 원판을 다른 기둥의 첫 번째 원판이 되도록 옮겼다. 하지만, 이번 하노이 타워는 한 기둥의 가운데 원판이 다른 기둥의 "가운데 원판"이 되도록 옮겨야 한다. 여기서 어떤 기둥의 가운데 원판은, 그 기둥에 쌓인 원판의 개수를 $n$이라고 할 때, $1+\left\lfloor\frac{n}{2}\right\rfloor$ 번째 원판을 말한다. 최대 이동 회수 $M = 980403$이 주어졌을 때, 디스크의 개수 $N$을 (코드를 제출하는 사람이) 정하고, 1번 기둥의 $N$개의 원판을 3번 기둥으로 옮기는 문제이다. ($N = 26$인 경우 만점이다.)
여러가지 관찰이 필요한 문제이다. 다음과 같은 관찰을 하나씩 해 보자.
관찰 1. 한 기둥의 가장 위에 있는 원판을 다른 기둥의 가장 위로 옮기려면, 해당 원판을 제외하고는 두 기둥에 다른 어떠한 원판도 존재하지 않아야 한다.
증명. $n=1$인 경우만 $1+\left\lfloor\frac{n}{2}\right\rfloor = 1$이 된다.
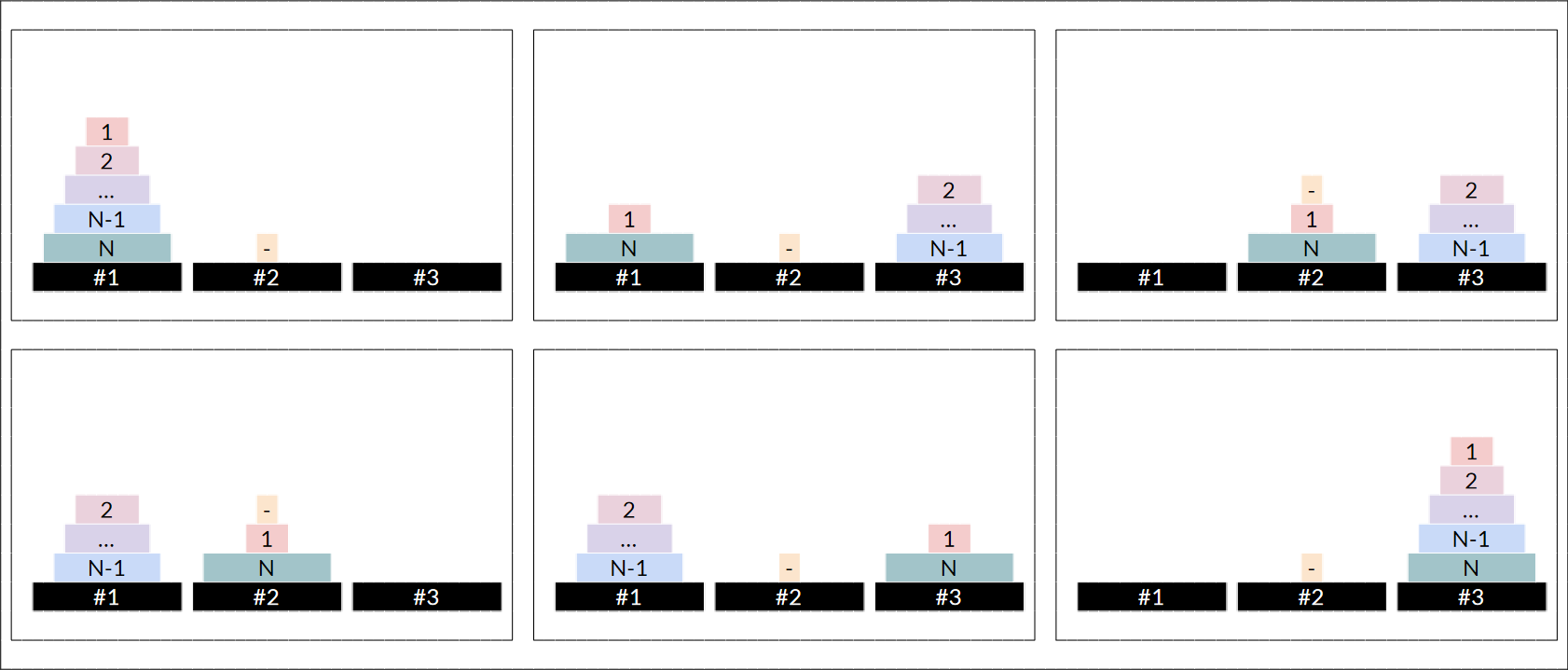
편의상 원판의 번호를 작은 것 부터 큰 것 까지 $1$부터 $N$까지의 번호를 붙이자. 여기서 다음과 같은 전략을 사용할 수 있다. 1번 기둥에서 3번 기둥으로 원판을 모두 옮기기 위해서는 $2$번 원판부터 $N$번 원판까지를 전부다 2번 기둥으로 옮긴다음에, 1번 기둥에서 3번 기둥으로 1번 원판을 옮기고, 2번 기둥에 놓인 $N-1$개의 원판을 다시 3번 기둥으로 옮겨야 한다.

일반적인 하노이 타워 문제는 나머지 원판들에 대해 재귀적으로 같은 방식으로 진행했겠지만, 이 문제는 다른 점이 있다. 바로, 1번 원판의 존재때문에 기둥을 빼내는 순서가 다르다는 점이다. 1~5번 원판이 쌓여있을 때 빠지는 순서는 3, 4, 2, 5(, 1)순이다. 하지만 2~5번 원판이 쌓여있을 때 빠지는 순서는 4, 3, 5, 2순이다. 즉, 어떤 기둥 위에 (고정되어서 빠지지 않는) 원판이 $0$개 있는지 $1$개 있는지에 따라서 과정이 다르게 된다. $a$, $b$, $c$번 기둥 위에 고정된 원판이 각각 $x$, $y$, $z$개 있는 상황에서 a번 기둥에서 c번 기둥까지 $N$개의 원판을 옮기는 과정을 $Mabc(N, a, b, c)$이라고 말하자. 가장 처음의 상황은 $M000(N, 1, 2, 3)$이고, $M000(N, a, b, c)$는 $M100(N-1, a, c, b)$를 수행하고, $a$에서 $c$로 1번 원판을 옮기고, $M001(b, a, c)$를 수행하게 된다. 이제 해당 기둥의 "가운데 원판"의 위치가 바뀐다.
관찰 2. 기둥 위에 고정된 원판이 1개 있는 경우, 가운데 원판을 $\left\lfloor\frac{n+1}{2}\right\rfloor$번 원판이라고 생각하면 된다. 또한, 해당 기둥의 가장 아래에 있는 원판을 옮기려면, 해당 기둥에는 고정된 원판과 가장 아래에 있는 원판을 제외하고, 남은 원판이 없어야 한다.
증명. 고정된 원판 1개를 제외하고 원판이 $n$개 있는 경우, 고정된 원판을 포함한 중심 위치는 $1+\left\lfloor\frac{n+1}{2}\right\rfloor$번째이다. 첫 번째인 고정된 원판을 제외하면, 중심 위치는 $\left\lfloor\frac{n+1}{2}\right\rfloor$번 원판이 된다. 여기서 $n \ge 1$ 일 때, 항상 $1 \le \left\lfloor\frac{n+1}{2}\right\rfloor \le n$을 만족하므로, 중심 원판은 항상 옮기려는 원판 중에 존재한다. 가장 아래쪽에 있는 원판을 꺼내려면, $n = \left\lfloor\frac{n+1}{2}\right\rfloor$ 이어야 하고, 이 경우는 $n=1$이다. 옮기려는 원판을 제외하고는 다른 원판이 존재하지 않는다.
이제 해당 과정을 기준으로 $M100(N, a, b, c)$상황을 생각해보자. ($M001$은 $M100$의 역순으로 진행된다.) 가장 아래에 있는 원판을 옮기는 과정을 생각해보자. 이도 마찬가지로, $a$번 기둥의 $N$번 원판을 제외한 원판들을 전부 $b$번 원판에 옮기고 $N$번 원판을 $c$번 원판에 옮긴 이후에, $b$번 기둥의 나머지 원판을 $c$번 기둥으로 옮기면 된다.
여기서, 과정을 잘 살펴보면 $a$번 기둥에서 마지막에 나오는 두 개의 1번 원판과 $N$번 원판을 옮길 때, $b$번 기둥을 거쳐갈 필요 없이 $c$번 기둥으로 두 원판을 차례로 옮길 수 있다는 것을 알 수 있다. ($a$번째 원판과 $c$번째 원판의 "가운데 원판"을 정의하는 홀짝성이 달라서 발생하는 일이다.) 그래서 과정을 바꿔서 $N-2$개의 기둥을 한번에 옮기는 것으로 문제를 풀 수 있다.

이제, 여기서 재귀적인 과정을 하려면 또 역시 자신 위와 아래에 있는 원판이 문제라는 것을 알 수 있다. 하지만 이 경우에는 중심 원판이 바뀌지 않기 때문에, 다음과 같은 관찰을 이용해서 재귀식을 그대로 사용할 수 있다.
관찰 3. 기둥 위에 고정된 원판이 X+K개, 아래쪽에 X개 있는 경우 가운데 원판은 기둥 위에 고정된 원판이 $K$개, 아래쪽에 $0$개 있는 경우와 같다.
증명. 원판이 $n$개 있는 경우, 고정된 원판을 포함한 중심 위치는 $1+\left\lfloor\frac{n+2X+K}{2}\right\rfloor$번째이다. $X+K$개의 고정된 원판을 제외하면, 중심 위치는 $1-K+\left\lfloor\frac{n+K}{2}\right\rfloor$번 원판이 된다. $K=0$일 때는, 위에서 $1+\left\lfloor\frac{n}{2}\right\rfloor$번째, $K=1$일 때는, 위에서 $\left\lfloor\frac{n+1}{2}\right\rfloor$번째 원판이다.
그래서 $1$번과 $N$번 원판을 더 이상 옮기지 않을 생각으로 같이 무시해주어도, 원반의 위치는 변하지 않는다. $M100(N, a, b, c)$는 $M100(N-2, a, c, b)$를 진행하고, $a$ 번 기둥에서 $c$ 번 기둥으로 원판을 두 번 옮기고, $M010(N-2, b, a, c)$를 진행해주면 된다.
이제 $M010$을 살펴보자. $M010$은 $M000$과 유사하지만, 가운데 원판에 따른 홀짝성을 고려해서 $M101(N-1, a, c, b)$를 진행하고 $a$번 기둥에서 $c$번 기둥으로 원판을 옮기고, $M101(N-1, b, a, c)$를 진행하면 된다. 하지만 이것이 최적이 아닌 경우는 위에 논의했던 대로 $a$ 번 기둥에서 $b$ 번 기둥에 홀짝성이 다른 점을 이용하면 한 번에 두 개의 원판을 옮길 수 있기 때문이다. 이를 이용해서 $a$ 번 기둥에서 $c$ 번 기둥으로 $2$번부터 $N-1$번 원판을 옮기고, $a$ 번 기둥에서 $b$ 번 기둥으로 $1$번과 $N$번 원판을 옮기고, $c$ 번 기둥에서 $a$ 번 기둥으로 $2$번부터 $N-1$번 원판을 옮기고, $b$ 번 기둥에서 $c$ 번 기둥으로 $1$번과 $N$번 원판을 옮기고 $a$ 번 기둥에서 $c$ 번 기둥으로 $2$번부터 $N-1$번 원판을 옮기면 된다.
...여기까지가 Jérémy Barbay가 arXiv[1602.03934]에 올린 "Bouncing Towers move faster than Hanoï Towers, but still require exponential time"라는 아티클에 설명되어 있는 사항이고, 이 아티클은 이 방법이 최적이라고 주장하지만, 이 아티클의 증명이 틀렸는지 이 문제가 만점을 받을 수 없는 문제인지, 위에 적힌 방법으로는 만점을 받을 수 없다.($N=25$일 때 $885\,735$번, $N=26$일 때 $1\,594\,323$번 움직인다.)
이 문제에서 만점을 받으려면, 해당 아티클의 증명의 틀린 부분을 찾으면서 위 문제의 설명에서 간과되어 있는 부분을 찾아야 하는데, $M010(N, a, b, c)$의 과정은 바깥에 있는 고정된 원판을 움직일 수 없는 것을 가정하고 있지만, 사실 고정된 원판을 움직이고 원래 위치로 돌려놓으면 된다!
다음과 같은 과정을 생각하자. $N$번 원판의 위치를 고려하지 않고 $1$번부터 $N-1$번까지의 원판을 $a$ 번 기둥에서 $b$ 번 기둥으로 옮겨놓는다. 그 후 $N$번 원반이 $a$ 번 기둥에 있으면 $c$ 번 기둥으로, $c$ 번 기둥에 있으면 $a$ 번 기둥으로 옮긴 다음에, 다시 $1$번부터 $N-1$번까지의 원판을 위 과정의 역순으로 $b$ 번 기둥에서 $c$ 번 기둥으로 옮겨놓는다. 이 경우 $M010(N, a, b, c)$는 (Notation을 확장해서 관찰 3에서 $K=-1$이라는 의미로) $M(-1)01(N-1, a, c, b)$를 진행하고 $N$번 원판의 $a$, $c$위치를 바꾼 이후에 $M10(-1)(N-1, b, a, c)$를 실행한다고도 볼 수 있겠다. 여기서 $K$가 $0$이나 $1$이 아닐 경우에는, 가운데 원판이 고정된 원판을 가리킬 수 있다는 점이고, 우리는 이 경우를 특별하게 허용하기로 했다.

위쪽에서 고정된 원판을 -로 표현했다. 아래쪽에서 고정된 원판은 +로 표현하자. $1$번부터 $N$번까지의 원판을 빼내는 과정의 마지막은 $2, +, 1$번 원판 순이 되어버렸다. 이 경우에도 $1$번 원판을 빼내려면 나머지 원판을 다 빼내야 하기 때문에, 나머지 $2$번부터 $N$번 원판까지를 생각해보자. 가장 빨리 빼내는 방법은 $2$번부터 $N$번까지의 원판을 한 개 이하를 제외하고 $b$ 번 기둥에 몰아놓은 이후에 1번 원판을 $c$ 번 기둥으로 옮기는 것이다. 여기서 한 개 이하의 원판을 제외하는 이유는, 한 개의 원판이 있어도 1번 원판이 $c$번 기둥으로 들어갈 수 있기 때문이다. 여기서 우리는 1번과 2번 다음으로 빼기 어려운 $N$ 번 원판을 $c$ 번 기둥에 같이 남기는 방식을 사용할 것이다.
$3$번 원판부터 $N$ 번 원판까지를 $c$ 번 기둥에 옮기고, $2$번과 $+$ 번 원판을 $b$ 번 기둥에 옮기다. 그리고 나머지 허용된 하나의 $N$ 번 기둥을 제외한 $3$번 부터 $N-1$번 원판을 $b$ 번 기둥에 옮긴다. 나머지는 재귀적으로 $M(-1)01(N-2, b, a, c)$를 호출해주면 된다.

이를 구현하면 $N=26$일 때 $972\,051$번 연산을 사용해서 원판을 전부 옮길 수 있고, 이는 $980\,403$이라는 제한 안에 들어가는 수이다.
아래는 풀이를 구현한 소스코드이다.
#1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#include <bits/stdc++.h>
using namespace std;
long long solve(int N)
{
long long ans = 0;
for(int i=-N+1; i<=N-1; ++i)
{
int j = sqrt(1LL*N*N-1LL*i*i-1);
ans += 2*j+1;
}
return ans;
}
int main()
{
int T; scanf("%d", &T);
for(int i=1; i<=T; ++i)
{
int N; scanf("%d", &N);
printf("Case #%d\n%lld\n", i, solve(N));
}
}
|
cs |
#2
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include <bits/stdc++.h>
using namespace std;
int solve(int K, vector<pair<int, int> > V)
{
sort(V.begin(), V.end());
long long minv = LLONG_MAX;
do
{
const int dx[] = {0, 0, 1, 2, 3, 3, 2, 1};
const int dy[] = {1, 2, 3, 3, 2, 1, 0, 0};
vector<int> xc, yc;
for(int i=0; i<8; ++i)
{
xc.push_back(V[i].first+dx[i]*K);
yc.push_back(V[i].second+dy[i]*K);
}
sort(xc.begin(), xc.end()); sort(yc.begin(), yc.end());
long long ans = 0;
for(int i=0; i<8; ++i)
ans += abs(xc[i]-xc[3])+abs(yc[i]-yc[3]);
minv = min(ans, minv);
}while(next_permutation(V.begin(), V.end()));
return minv;
}
int main()
{
int T; scanf("%d", &T);
for(int i=1; i<=T; ++i)
{
int K; scanf("%d", &K);
vector<pair<int, int> > V;
for(int j=0; j<8; ++j)
{
int a, b; scanf("%d%d", &a, &b);
V.emplace_back(a, b);
}
printf("Case #%d\n%d\n", i, solve(K, V));
}
}
|
cs |
#3
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include <bits/stdc++.h>
using namespace std;
long long solve(int N, int K, vector<vector<long long> > A)
{
vector<vector<long long> > D(N+2*K, vector<long long>(N+2*K)), U = D, R = D, L = D, ans = D;
auto get = [N, K](const vector<vector<long long> >& V, int x, int y)
{
if(x < 0 || x >= N+2*K || y < 0 || y >= N+2*K) return 0LL;
return V[x][y];
};
long long ret = 0;
for(int i=0; i<N+2*K; ++i)
for(int j=0; j<N+2*K; ++j)
{
D[i][j] = get(D, i-1, j-1) - get(A, i-K, j-1) + get(A, i, j+K-1);
U[i][j] = get(U, i-1, j+1) - get(A, i-1, j+K) + get(A, i+K-1, j);
}
for(int i=0; i<N+2*K; ++i)
for(int j=0; j<N+2*K; ++j)
{
R[i][j] = get(R, i-1, j) - get(D, i-1, j) + get(U, i, j);
L[i][j] = get(L, i-1, j) - get(U, i-K, j-K+1) + get(D, i+K-1, j-K+1);
}
for(int i=0; i<N+2*K; ++i)
for(int j=0; j<N+2*K; ++j)
ret = max(ret, (ans[i][j] = get(ans, i, j-1) - get(L, i, j-1) + get(R, i, j)));
return ret;
}
int main()
{
int T; scanf("%d", &T);
for(int t=1; t<=T; ++t)
{
int N, K; scanf("%d%d", &N, &K);
vector<vector<long long>>V(N+2*K, vector<long long>(N+2*K));
for(int i=K; i<N+K; ++i)
for(int j=K; j<N+K; ++j)
scanf("%lld", &V[i][j]);
printf("Case #%d\n%lld\n", t, solve(N, K, V));
}
return 0;
};
|
cs |
#4 (node가 패턴의 길이만큼의 배열을 담고 있어서, 시간복잡도가 더 크나, 통과 가능하다)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
|
#include <bits/stdc++.h>
using namespace std;
vector<int> convert(string s)
{
vector<int> res(s.size());
vector<int> arr(26, -1);
for(int i=0; i<(int)s.size(); ++i)
{
int c = s[i]-'a';
if(arr[c] == -1) res[i] = 0;
else res[i] = i - arr[c];
arr[c] = i;
}
return res;
}
const int PATTERN_MAXL = 500;
const int PATTERN_TOTLEN = 30000;
struct Node
{
int L, cnt;
int next[PATTERN_MAXL+1];
int fail;
} NODE[PATTERN_TOTLEN+1];
int tp = 0;
void reset(){ tp = 0; }
int new_node()
{
NODE[tp].L = NODE[tp].cnt = 0;
memset(NODE[tp].next, -1, sizeof NODE[tp].next);
NODE[tp].fail = -1;
return tp++;
}
int get_fail(int node, int c)
{
if(node == -1) return 0;
if(c > NODE[node].L) c = 0;
if(NODE[node].next[c] != -1) return NODE[node].next[c];
return get_fail(NODE[node].fail, c);
}
int put(int node, int c)
{
if(NODE[node].next[c] != -1) return NODE[node].next[c];
int ret = new_node();
NODE[ret].L = NODE[node].L + 1;
NODE[node].next[c] = ret;
return ret;
}
vector<int> fail_order;
void forward_fail()
{
fail_order.clear();
queue<int> Q; Q.push(0);
while(!Q.empty())
{
int n = Q.front(); Q.pop();
fail_order.push_back(n);
for(int i=0; i<=NODE[n].L; ++i)
{
int m = NODE[n].next[i];
if(m != -1)
{
Q.push(m);
NODE[m].fail = get_fail(NODE[n].fail, i);
}
}
}
}
void back_prop()
{
reverse(fail_order.begin(), fail_order.end());
for(int n: fail_order)
if(n != 0)
NODE[ NODE[n].fail ].cnt += NODE[n].cnt;
}
vector<int> solve(vector<int> s, vector<vector<int>> V)
{
reset();
int root = new_node();
vector<int> patNodes;
for(const auto& pat: V)
{
int cur = root;
for(auto v: pat)
cur = put(cur, v);
patNodes.push_back(cur);
}
forward_fail();
int cur = root;
for(auto v: s)
{
cur = get_fail(cur, v);
NODE[cur].cnt++;
}
back_prop();
for(auto& v: patNodes) v = NODE[v].cnt;
return patNodes;
}
int main()
{
ios::sync_with_stdio(false);
int T; cin >> T;
for(int t=1; t<=T; ++t)
{
int N, K; string s; cin >> N >> K >> s;
vector<vector<int>> V(K);
for(auto& v: V)
{
string s; cin >> s; v = convert(s);
}
vector<int> res = solve(convert(s), V);
long long ans = 0;
for(int i=1; i<=K; ++i) ans += res[i-1]*i;
cout << "Case #" << t << endl << ans << endl;
}
}
|
cs |
#5
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62 |
#include <string>
#include <iostream>
using namespace std;
string op[3] = {"*AB", "C*D", "EF*"};
string B1(int, int, int, int), B2(int, int, int, int), C(int, int, int, int);
string D1(int, int, int, int), D2(int, int, int, int); string A(int N, int a, int b, int c)
{
if(N == 0) return string();
return B1(N-1, a, c, b) + op[a][c] + B2(N-1, b, a, c);
}
string B1(int N, int a, int b, int c)
{
if(N == 0) return string();
if(N == 1) return string({op[a][c]});
return B1(N-2, a, c, b) + op[a][c] + op[a][c] + C(N-2, b, a, c);
}
string B2(int N, int a, int b, int c)
{
if(N == 0) return string();
if(N == 1) return string({op[a][c]});
return C(N-2, a, c, b) + op[a][c] + op[a][c] + B2(N-2, b, a, c);
}
string C(int N, int a, int b, int c)
{
if(N == 0) return string();
if(N == 1) return string({op[a][c]});
if(N == 2) return string({op[a][b], op[a][c], op[b][c]});
return D1(N-1, a, c, b) + (N%4 < 2 ? op[a][c]: op[c][a]) + D2(N-1, b, a, c);
}
string D1(int N, int a, int b, int c)
{
if(N == 0) return string();
if(N == 1) return string({op[a][b], op[a][c]});
if(N == 2) return string({op[a][c], op[a][b], op[a][c]});
return C(N-2, a, b, c) + op[a][b] + op[a][b] + C(N-3, c, a, b) + op[a][c] + D1(N-2, b, a, c);
}
string D2(int N, int a, int b, int c)
{
if(N == 0) return string();
if(N == 1) return string({op[a][c], op[b][c]});
if(N == 2) return string({op[a][c], op[b][c], op[a][c]});
return D2(N-2, a, c, b) + op[a][c] + C(N-3, b, c, a) + op[b][c] + op[b][c] + C(N-2, a, b, c);
}
string solve(int N)
{
return A(N, 0, 1, 2);
}
int main()
{
int N = 26;
cout << "Case #1" << endl << N << endl << solve(N) << endl;
}
|
cs |
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| SCPC 2022 본선 풀이 (0) | 2022.09.03 |
|---|---|
| SCPC 2022 2차 풀이 (0) | 2022.08.06 |
| SCPC 2021 1차 풀이 (0) | 2021.07.17 |
| 테스트 데이터 만들기: Anti-Hash test / Anti-Javasort test (0) | 2018.10.11 |
| Simple Cubic General Maximum Matching Algorithm (0) | 2018.03.22 |